- Network Sites:
-
 EEPower Day is a free 1-day virtual conference. Learn More
EEPower Day is a free 1-day virtual conference. Learn More
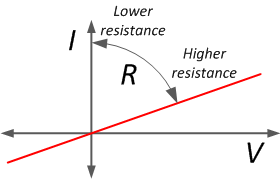 Ohm’s law states that the electrical current through a conductor is proportional to the potential difference across it. Furthermore, the electrical resistance of the conductor is constant. This leads to the mathematical equation:
Ohm’s law states that the electrical current through a conductor is proportional to the potential difference across it. Furthermore, the electrical resistance of the conductor is constant. This leads to the mathematical equation:
$$R = \frac{V}{I}$$
where R the resistance in ohms (Ω), V the voltage in volts (V), and I is the current in amperes (A). To illustrate: a resistor of 1 Ω subjected to a current of 1 A has a voltage difference of 1 V across its terminals. The equation is named after Georg Ohm. In 1827 he published his findings that form the basis of the formula that is used today. He performed a large series of experiments that showed the relation between applied voltage and current through a conductor. The law is therefore empirical. Although Ohm’s law is one of the fundamentals of electrical engineering, at the time of publication it was received with criticism. The ohm is adopted as the official SI unit for electrical resistance. Gustav Kirchhoff (known from Kirchhoff’s circuit laws) made a generalization that is used more often in physics:
$$\sigma = \frac{J}{E}$$
where σ is the conductivity parameter (material specific), J is the current density, and E is the electric field.
Resistors are passive elements that introduce resistance to the flow of electric current in a circuit. A resistor that functions according to Ohm’s law is called an Ohmic resistor. When current passes through an Ohmic resistor, the voltage drop across the terminals is proportionally to the magnitude of resistance. Ohm’s formula is also valid for circuits with varying voltage or current, so it can be used for alternating current (AC) circuits as well. For capacitors and inductors, Ohm's law cannot used since their I-V curves are inherently not linear (not Ohmic).
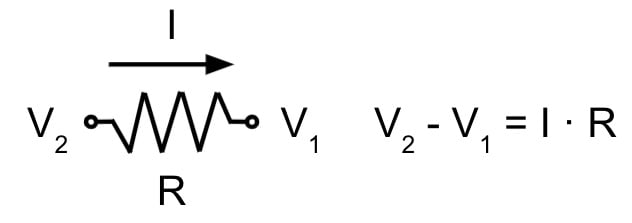
Ohm’s formula is valid for circuits with multiple resistors that can be connected in series, parallel or both. Groups of resistors in series or parallel can be simplified with an equivalent resistance. The articles Resistors in Series and Resistors in Parallel describe this process in more detail.
|
Georg Simon Ohm (1789-1854)
In 1827, German physicist Georg Simon Ohm published his complete theory of electricity with the title The Galvanic Circuit Investigated Mathematically. He found that the voltage drop over a part of a circuit is the product of the current through and the resistance of that part. This formed the basis of the law that we use today. The law is one of the fundamental relations for resistors. His colleagues didn’t appreciate his findings, and the law was not easily accepted. Ohm was a teacher at a gymnasium (high school) in Cologne at that time, and he decided to resign. Ohm became professor of experimental physics at the University of Munich. Later in his life, he was finally recognized for his work and received the Copley Medal in 1841 from the Royal Society. |
Ohm's formula can be used when two of three variables are known. The relation between resistance, current and voltage can be written in different ways. To remember this, the Ohm triangle calculator shown in the figure might be helpful. Two examples below will show the use of the triangle calculator and Ohm's law.
$$R = \frac{V}{I}$$
or
$$V = I · R $$
or
$$I = \frac{V}{R}$$
Examples Using Ohm's Law |
|
|
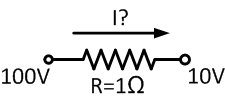
Consider a 1 Ω resistor in a circuit with a voltage drop from 100 V to 10 V across its terminals. What is the current through the resistor? The triangle reminds us that: $$I = \frac{V}{R} = \frac{100 - 10}{1} = 90 A$$ |
 |
|
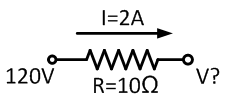
Consider a 10 Ω resistor in a circuit subject to a current of 2 A and a voltage of 120 V. What is the voltage drop across the resistor? Using the triangle shows us that: $$V = I · R = 2 · 10 = 20 V$$ The voltage drop across the resistors is 20 V; therefore, the voltage at the end terminal is 120 - 20 = 100 V. |
 |
A resistor dissipates power when a current passes through it. The energy is released in the form of heat. The power is a function of the current I and the applied voltage V:
$$P = V · I$$
where P is the power in watts (W). Combined with Ohm’s law, the power law can be rewritten into:
$$P = R · I^2$$
or
$$P = \frac{V^2}{R}$$
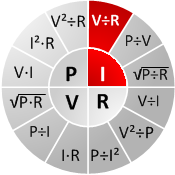
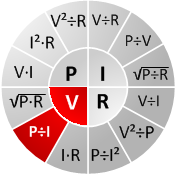
Ideal resistors dissipate all energy and do not store electric or magnetic energy. Each resistor has a limit to the power that can be dissipated without resulting in damage. This is called the power rating. Ambient conditions can reduce this value. For example, an enclosure around the resistor or a higher ambient temperature will reduce the amount of energy the resistor can dissipate. This effect is called derating, and can be visualized with a power derating chart. In practice, resistors seldom have an indicated power rating. However, the majority of resistors are rated at 1/4 or 1/8 watt. The circle diagram helps to quickly find the relation between electric power, current, voltage and resistance. For each of the four parameters, the figure shows how to calculate the desired parameter value when given the other circuit values.
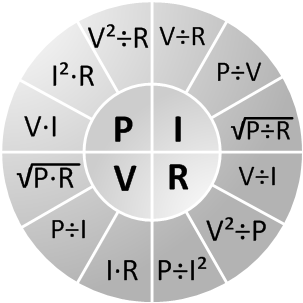
Below, several examples of Ohm’s law problems are given.
Examples |
||
| What must be the minimal power rating of this resistor?
Answer: According to the wheel equations: $$P = I^2 · R = (0.100)^2 · 50 = 0.5 W$$ The minimal power rating should be at least 0.5 W, but it is recommended to select a resistor with a rating well above this value for extra reliability and lifetime. |
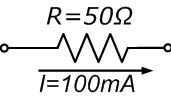 |
 |
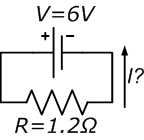
| What is the current in the circuit?
This is a basic example of Ohm’s law. Voltage and resistance are known, so we can calculate current with the equation: $$I = \frac{V}{R} = \frac{6}{1.2} = 5 A$$ |
 |
 |
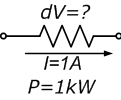
| An electric heater (resistor) with a consumption of 1 kW is connected in a circuit with 8 A current. What is the voltage drop over the heater?
The voltage can be calculated from the power and the current with the formula: $$V = \frac{P}{I} = \frac{1000}{8} = 125 V$$ |
 |
 |
The resistance value in ohms is often marked with a color code on the resistor. The combination of colors tells the value as well as the tolerance of the resistor. For more information about this topic, refer to the resistor color code.
I really enjoyed the webpage mentioned above, but in it you say that George Ohm taught in a gymnasium. He did, but in German a gymnasium is a place of higher education, not a place of physical improvement. Perhaps you should alter the site to reflect this. But apart from this I really appreciate the site. the clear and concise writing manages to be both informative and not at all patronising. Walking the tightrope between being too technical and not being technical enough is a difficult trick to pull off, but the author of this page manages it spectacularly.
Ohms Law Calculator is a simple and easy-to-use app that helps you with all types of calculations related to Ohm’s Law.
Download this app now!
https://play.google.com/store/apps/details?id=com.ijtech.ohm_law