- Network Sites:
-
 EEPower Day is a free 1-day virtual conference. Learn More
EEPower Day is a free 1-day virtual conference. Learn More
The function of a resistor is to oppose the electric current through it. This is called electrical resistance, and is measured in the unit ohm (represented by the Greek uppercase letter omega, Ω). The resistance can be calculated with Ohm's law, when the voltage drop across the resistor and the current through the resistor are known:
$$R = \frac{V}{I}$$
The resistance of a resistor is dependent on its material and shape. Some materials have a higher resistivity, thereby resulting in a higher resistance value. The resistance value is often printed on the resistor with a alphanumeric code for SMD resistors or in the form of a color code for through-hole resistors.
The concept of current, voltage and resistance can be explained by a hydraulic analogy. A flow of water through a pipe is restricted by a constriction. This causes a pressure drop after the constriction. The flow of water is equivalent to electric current. The pressure drop is equal to the voltage drop. The constriction is equivalent to the resistor and has a certain resistance. The resistance is proportional to the voltage or pressure drop for a given current.
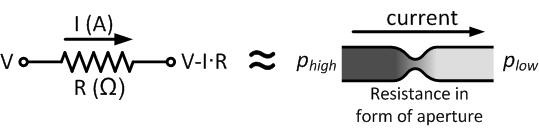
In the hydraulic example, the resistance can be increased by for example reducing the diameter of the constriction. For a resistor or wire, the resistance is in general dependent on the material and the geometrical shape. The influence of the geometrical shape can easily be explained by using the hydraulic example. A long and narrow tube will have a higher resistance than a short and wide tube.
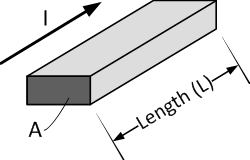 Resistance of a rectangular cross-section resistor with cross-sectional area A and length L.
Resistance of a rectangular cross-section resistor with cross-sectional area A and length L.
The resistance property of a material is called resistivity. The electrical resistance of a resistor is proportional to the resistivity of the material. For a rectangular cross-section resistor the resistance R is given by:
$$R = \frac{\rho · l}{A}$$
where ρ is the resistivity of the resistor material (Ω·m), l is the length of the resistor along direction of current flow (m), and A is the cross-sectional area perpendicular to current flow (m2). Resistivity is a property of materials. For many materials the resistivity is constant, and V and I are directly proportional to each other. Materials that meet this characteristic are called Ohmic materials. Good resistor materials have resistivity’s between 2·10-8 and 200·10-8 Ω·m.
The equivalent resistance of resistors in series is equal to the sum of each resistor:
$$R_{eq} = \sum_{i=1}^n R_i = R_1 + R_2 + \dots + R_n$$
The current through each resistor in series is equal, but the voltage is not. For a more detailed explanation and practical examples, refer to the article resistors in series. Sometimes the desired value is not available with standard preferred values. Instead, to create the desired resistance value, two resistors can be connected in series or parallel.
The equivalent resistance of resistors in parallel can be calculated with the following formula:
$$\frac{1}{R_{eq}} = \sum_{i=1}^{n} \frac{1}{R_i} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n} $$
The voltage across each resistor in parallel is equal, but the current is not. For a more detailed explanation and practical examples, refer to the article resistors in parallel.