- Network Sites:
-
 EEPower Day is a free 1-day virtual conference. Learn More
EEPower Day is a free 1-day virtual conference. Learn More
A capacitor is a two-terminal passive electrical component that can store electrical energy in an electric field. This effect of a capacitor is known as capacitance. Whilst some capacitance may exists between any two electrical conductors in a circuit, capacitors are components designed to add capacitance to a circuit. The capacitor was originally known as a condenser or condensator but is not widely used nowadays.
The ability of a conducting body to accumulate charge is known as capacitance. The capacitance value of a capacitor is represented by the formula:
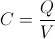
where C is the capacitance, Q is the amount of charge stored, and V is the voltage between the two electrodes. One plate equals the amount of charge on the other plate of a capacitor in real life circuits the amount of charge on, but these two charges are of different signs. By examining this formula we can deduce that a 1F (Farad) capacitor holds 1C (Coulomb) of charge when a voltage of 1V (Volt) is applied across its two terminals.
In constructing a capacitor, there are three basic factors that needs to be determined. All of these factors dictate capacitance by affecting the amount of electric field flux (relative difference of electrons between plates) that will develop for a given amount of electric field force (voltage between the two plates):
All other factors considered equal, greater plate area means greater capacitance; the lesser plate area means lesser capacitance.
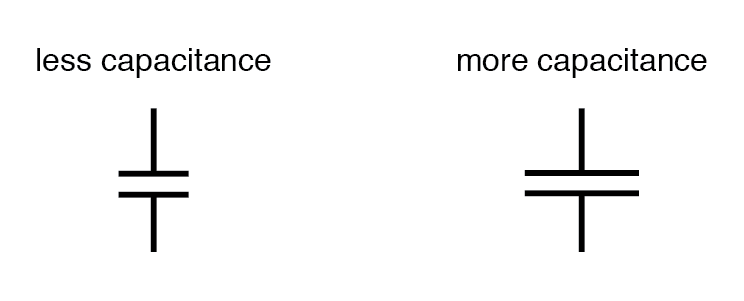
All other factors considered equal, the farther plate spacing gives less capacitance; closer plate spacing gives greater capacitance.
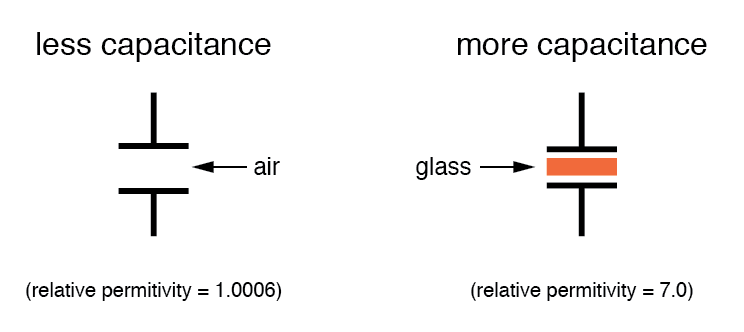
All other factors considered equal, greater permittivity of the dielectric gives greater capacitance; less permittivity of the dielectric gives less capacitance.
Dielectric materials are essentially insulators, which means that no current can flow through the material even when voltage is applied. However, some changes happen at the atomic scale. When a dielectric material is applied voltage across it, it becomes polarized.
Here are some examples of Dielectric materials with its Relative Permittivity/dielectric constant:
| Material | Relative permittivity (dielectric constant) |
| Vacuum | 1.0000 |
| Air | 1.0006 |
| PTFE, FEP ("Teflon") | 2.0 |
| Polypropylene | 2.20 to 2.28 |
| ABS resin | 2.4 to 3.2 |
| Polystyrene | 2.45 to 4.0 |
| Waxed paper | 2.5 |
| Transformer oil | 2.5 to 4 |
| Hard rubber | 2.5 to 4.80 |
| Wood (oak) | 3.3 |
| Silicones | 3.4 to 4.3 |
| Bakelite | 3.5 to 6.0 |
| Quartz, fused | 3.8 |
| Wood (maple) | 4.4 |
| Glass | 4.9 to 7.5 |
| Castor oil | 5.0 |
| Wood (birch) | 5.2 |
| Mica, muscovite | 5.0 to 8.7 |
| Glass-bonded mica | 6.3 to 9.3 |
| Porcelain, Steatite | 6.5 |
| Alumina | 8.0 to 10.0 |
| Distilled water | 80.0 |
| Barium-strontium-titanite | 7500 |
An electric field is a special state that exists in the space around an electrically charged particle. All charged particles placed in the electric field are affected by this “special state. The true nature of electric fields and electric charges are still unknown to scientists, but we can still use known equations to measure and predict the effects of an electric field.

Where E is the electric field, F is the force exerted on a particle introduced into the field and q is the charge of the particle. The unit for electric field is volts per meter [V·m-1] or newtons per coulomb [N·C-1].
The quality factor or Q factor of a capacitor, represents the efficiency of a given capacitor in terms of its energy losses. The Q factor is not a constant value and changes significantly with frequency.
Although most applications do not have to take the Q factor into serious consideration, and standard capacitors may be used in those applications, Q factor is one of the most important characteristics of a capacitor in designing RF circuits.
At RF frequencies, the ESR increases with frequency due to the so called “skin effect. Along with the increase in ESR, dissipative losses increase as well. This is why RF circuits use high-Q capacitors, to greatly help reduce high-frequency losses.